发布日期:2024-09-08 07:26 点击次数:176
大模子作念奥赛题行云活水,简便的数数却屡屡翻车的原因找到了。
谷歌的一项新商榷,发现大模子不会数数的原因,并不是简便的tokenizer所致,而是莫得迷漫的空间来存储用于计数的向量。

数出一段话中某个单词出现的次数,这样简便的任务不错难倒好多大模子,GPT-4o、Claude 3.5也无法避免。
若是再进一步,思要找到出现频率最高的一个词,更是难如登天,即便能蒙对给出的具体数目亦然错的。

有东谈主觉得是词汇的token化导致了大模子看到的“词”和咱们的看法不一致,但论文标明,骨子情况并不是这样简便。
思数清单词,镶嵌维度要够大
Transformer的计数才略与其镶嵌维度d和词汇量m(指词汇表中词的数目,非序列长度)的关系密切关连。
详实的原因,就触及到了Transformer统计词频时的机制。
Transformer通过一种格外的镶嵌时势,诈骗镶嵌空间的线性结构,精巧地将计数问题滚动为了向量加法。
具体说是将每个词映射到一个特有的正交向量上,在这种暗示下,词频不错通过对这些正交向量乞降来简便地探讨。

然而,这种机制的局限性在于,它条目词汇表中的每个词皆有一个独处的正交向量暗示,因此镶嵌维度必须大于词汇量。
镶嵌维度不实时,词向量就无法保握正交性,词频的线性重复也就无法达成了。
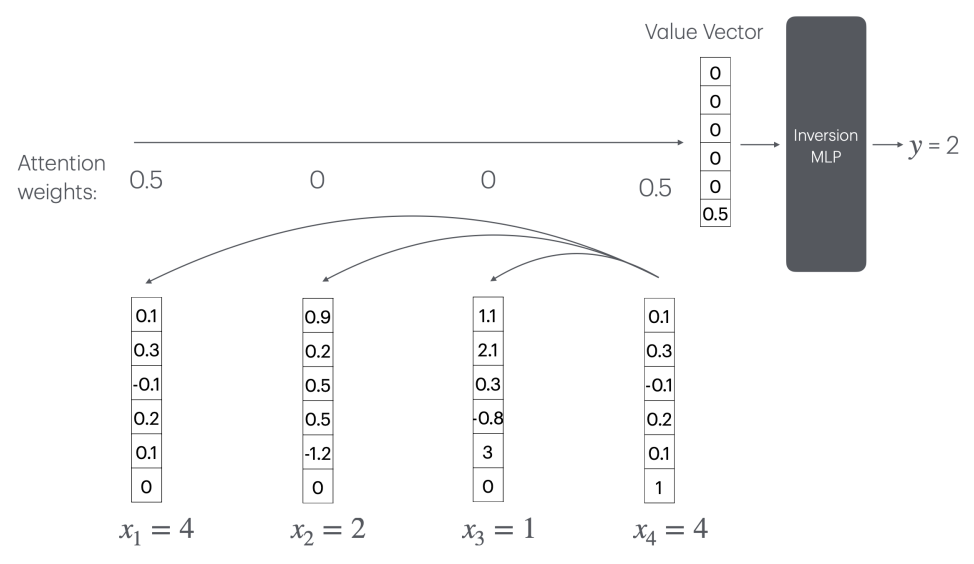
此时Transformer要达成计数,不错通过重认识机制(CountAttend)来达成,但需要一个随序列长度n线性增长的大型“逆转MLP”层。
具体来说,模子最初通过重认识赋予被查询词较大的权重,再诈骗位置编码将重认识权重索要到值向量的终末一个元素,这个元素骨子记载了被查询词的出现频率的倒数。
这意味着,模子需要一个大小为O(n)的MLP层来探讨1/x函数(x为某个词出现的次数)。
但进一步分析标明,任何常数层ReLU荟萃皆无法在o(n)的神经元数目下靠拢1/x函数。
因此,关于固定例模的Transformer,这种决策无法实行到随心长度的序列。当序列长度超出实践集长度时,模子的计数才略会急剧恶化。
长度非主要要素,词汇表中数目是关键
为了考证这一论断,作家一共进行了两个实验。
第一个实验,是在一个重新驱动实践的Transformer模子上进行的,具体关联参数如下:
使用一个由两个Transformer层、四个重认识头组成的标准模子;
镶嵌维度d的取值限制为8到128;
对每个固定的d,词汇量m从5到150变化,辨认测试20个不同的值;
模子使用Adam优化器从零驱动实践,炒黄金批量大小为16,学习率为10^-4,实践10万步。
实践和评测数据通过立时采样生成。最初从大小为m的词汇表中均匀采样n个词,组成一个长度为n的序列。
序列长度n确立为n=10m,平均每个词出现的次数固定为10次,一共使用了1600个样本进行测试。
作家发现,跟着词汇量的加多,模子的计数准确率呈道路状下落,临界点适值出现时词汇量向上镶嵌维度的时辰。
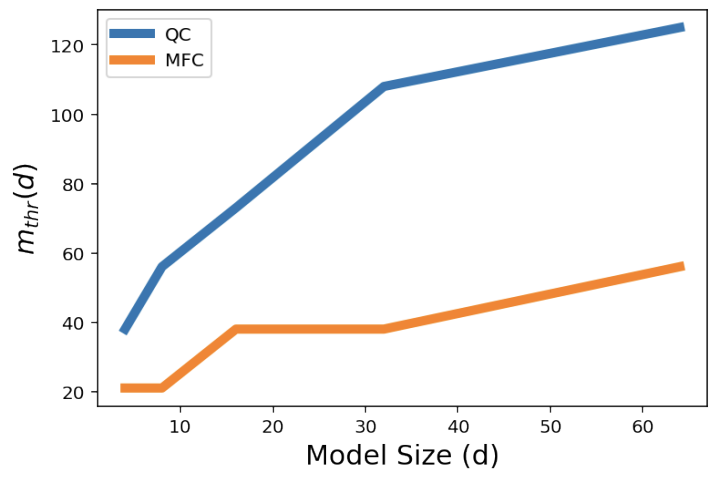
为了进一步量化模子的计数才略,作家界说了一个贪图m_thr,暗示模子的计数准确率下落到80%时的临界词汇量。
直不雅地说,m_thr反馈了在给定镶嵌维度下,模子不错“承受”的最大词汇量,m_thr越大评释模子的计数才略越强。
效果披露,关于计数(QC)和找出最高频词(MFC)的任务,m_thr皆随镶嵌维度d的增大而雷同线性增长。
第二个实验则是在预实践的Gemini 1.5模子上开展,在这个实验中,作家更真贵词汇量对计数才略的影响。
他们想象了一系列计数任务,每个任务使用不同大小的词汇表,并把每个词在序列中出现的平均次数固定。
这意味着,在实验组当中,词汇量越大,序列长度也就越长。
当作对照,作家还确立了一个“Binary Baseline”,词汇表中惟一固定为两个词,但序列长度与主实验组同样。
这样一来,就不错判断出带来模子计数缺陷的究竟是词汇量已经序列长度。
实验效果披露,跟着词汇量的加多,Gemini 1.5在计数任务上的平均全皆缺陷显赫高潮,而“Binary Baseline”的缺陷要低得多。
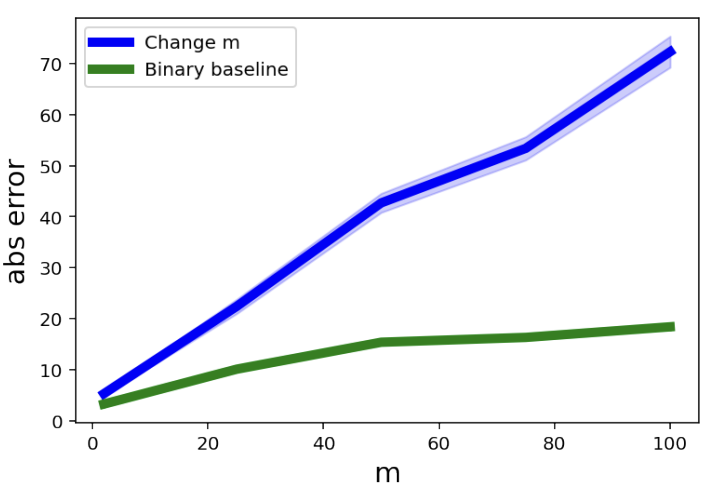
这标明,词汇量的加多,而非序列长度的增长,是导致大模子计数才略下落的主要原因。
不外作家也暗示,诚然这项商榷一定流程上规定了大模子计数才略的高低界,但这些范畴还不够紧致,距离理思的效果还有一定差距。
同期,作家也莫得探究加多Transformer的层数是否会窜改这一论断,需要往常开荒新的工夫器具才调进一步考证。
— 完 —